設(shè)隨機(jī)過(guò)程X(t)與Y(t)，t∈T不相關(guān)，試用它們的均值函數(shù)與協(xié)方差函數(shù)來(lái)表示隨機(jī)過(guò)程

Z(t)=a(t)X(t)+b(t)Y(t)+c(t)，t∈T

的均值函數(shù)和自協(xié)方差函數(shù)，其中a(t)，b(t)，c(t)是普通的函數(shù)．

給定隨機(jī)過(guò)程{X(t)，t∈T}，x是任一實(shí)數(shù)，定義另一個(gè)隨機(jī)過(guò)程

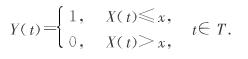
試將Y(t)的均值函數(shù)和自相關(guān)函數(shù)用隨機(jī)過(guò)程X(t)的一維和二維分布函數(shù)來(lái)表示．

設(shè){Y(t)=tX(t)，t∈T}，其中{X(t)，t∈T}為隨機(jī)過(guò)程，且m_Y(t)，R_X(t₁,t₂)已知。試求隨機(jī)過(guò)程Y(t)的均值函數(shù)m_Y(t)與自協(xié)方差函數(shù)C_Y(t₁,t₂)。

設(shè)Y(t)=Xt+a,t∈T，其中X為隨機(jī)變量，a為常數(shù)，且E(X)=u，D(X)=σ²，試求隨機(jī)過(guò)程{Y(t)，t∈T}的均值函數(shù)與自協(xié)方差函數(shù)。

設(shè)隨機(jī)過(guò)程{Y(t)=X(t)+φ(t)，t∈T}，其中φ(t)為普通實(shí)函數(shù)，X(t)為隨機(jī)過(guò)程，且已知mX(t)，C_X(t₁，t₂)，試求Y(t)的均值函數(shù)m_Y(t)，均方值函

數(shù)φ_Y²(t)，方差函數(shù)D_Y(t)，自相關(guān)函數(shù)R_Y(t₁,t₂)與自協(xié)方差函數(shù)C_Y(t₁,t₂)。

設(shè)Z(t)=X(t)+iY(t)是一復(fù)隨機(jī)過(guò)程，且EX(t)，EY(t)存在，則定義其均值與協(xié)方差函數(shù)為

EZ(t)=EX(t)+iEY(t)

若E|Z(t)|²＜+∞時(shí)，則稱Z(t)是一復(fù)二階矩過(guò)程。

試證：若Z(t)=X(t)+iY(t)為一復(fù)二階矩過(guò)程時(shí)有

設(shè)隨機(jī)過(guò)程x(t)的均值為μ_x(t)，自相關(guān)函數(shù)為r_x(t_j，t_k)。若有隨機(jī)過(guò)程y(t)=a(t)x(t)+b(t)，其中a(t)、b(t)是確知函數(shù)。求隨機(jī)過(guò)程y(t)的均值和自相關(guān)函數(shù)。

設(shè){X(t)=φ(t，A)，t∈T}，其中φ(t,A)為給定的函數(shù)，A是密度為f(x)的隨機(jī)變量。試求隨機(jī)過(guò)程X(t)的均值函數(shù)及協(xié)方差函數(shù)。

統(tǒng)計(jì)獨(dú)立的平穩(wěn)隨機(jī)過(guò)程X(t)和Y(t)，均值皆為0方差均為1，有隨機(jī)過(guò)程Z(t)=X(t)*Y(t)。

1.判斷Z(t)是否平穩(wěn).2.計(jì)算Z(t)的平均功率、均值、方差。